%%html
<style type="text/css">
input.good:checked + label {color: green}
input.bad:checked + label {color: red}
input.good:checked + label::after {color: green; content: ' Õige vastus!'}
input.bad:checked + label::after {color: red; content: ' Vale vastus!'}
</style>

Lineaarne kahemõõtmeline süsteem ja tema püsipunktid¶

Üldine skeem¶

Kui on antud lineaarne kahemõõtmeline dünaamiline süsteem, siis on kindlaks püsipunktiks $\underline{x}_* = (0, 0)$. See tööleht näitab, kuidas saab määrata selle püsipunkti stabiilsust. Alljärgnev juhend võib kasuks olla.

Kirjutage oma süsteemi kujul $\underline{\dot{x}} = \underline{\underline{M}} \cdot \underline{x}$ maatriksiga $\underline{\underline{M}}$, ehk kujul

$$\begin{pmatrix}\dot{x}_1 \\ \dot{x}_2\end{pmatrix} = \begin{pmatrix}a & b \\ c & d\end{pmatrix} \cdot \begin{pmatrix}x_1 \\ x_2\end{pmatrix}$$
Leidke karakteristlikku võrrandit

$$0 = |\underline{\underline{M}} - \lambda\underline{\underline{1}}| = \begin{vmatrix}a - \lambda & b \\ c & d - \lambda\end{vmatrix} = (a - \lambda)(d - \lambda) - bc = \lambda^2 - \tau\lambda + \Delta,$$

kus $\tau = a + d$ on jälg ja $\Delta = ad - bc$ on determinant.
Arvutage omaväärtusi

$$\lambda_{1,2} = \frac{\tau}{2} \pm \sqrt{\frac{\tau^2}{4} - \Delta}.$$

Siin $\delta = \frac{\tau^2}{4} - \Delta$ on diskriminant.

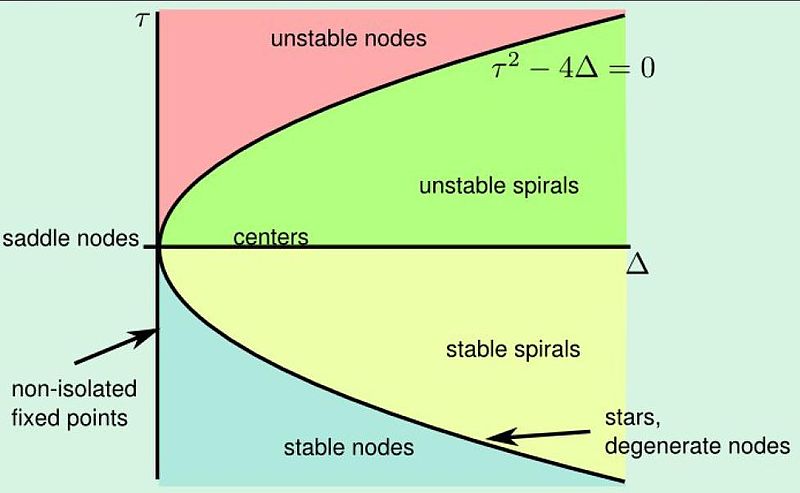
Püsipunkti $\underline{x}_* = (0, 0)$ tüüp sõltub maatriksi determinandist $\Delta$ ja jäljest $\tau$. Seda iseloomustada aitab selline skeem:

Püsipunkti tüübi iseloomustamine

NumPy ja PyPlot aitavad meid püsipunkte visualiseerimiseks.

%matplotlib inline

import numpy as np
import matplotlib
import matplotlib.pyplot as plt
from IPython.display import display, Markdown

Alljärgnev funktsioon…

…arvutab $\tau$, $\Delta$, $\delta$;
…arvutab omaväärtusi;
…joonistab faasiportreet.

def fixed(a, b, c, d):
    tr = a + d
    det = a * d - b * c
    dis = tr ** 2 / 4.0 - det

    display(Markdown('Maatriks: $\\begin{pmatrix}%f & %f \\\\ %f & %f\\end{pmatrix}$' % (a, b, c, d)))
    display(Markdown('Jälg: &tau; = %f' % tr))
    display(Markdown('Determinant: &Delta; = %f' % det))
    display(Markdown('Diskriminant: &delta; = %f' % dis))
    if dis > 0:
        l1 = tr / 2 + np.sqrt(dis)
        l2 = tr / 2 - np.sqrt(dis)
        display(Markdown('Omaväärtused: &lambda;<sub>1</sub> = %f, &lambda;<sub>2</sub> = %f' % (l1, l2)))
    elif dis < 0:
        re = tr / 2
        im = np.sqrt(-dis)
        display(Markdown('Omaväärtused: &lambda;<sub>1</sub> = %f + %fi, &lambda;<sub>2</sub> = %f + %fi' % (re, im, re, -im)))
    else:
        display(Markdown('Omaväärtused: &lambda;<sub>1,2</sub> = %f' % (tr / 2)))

    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.set_aspect('equal', 'box')
    ax.set_xlabel('x')
    ax.set_ylabel('y')

    X = np.linspace(-9, 9, 101)
    Y = np.linspace(-9, 9, 101)
    XX, YY = np.meshgrid(X, Y)
    DX = a * XX + b * YY
    DY = c * XX + d * YY
    ax.streamplot(XX, YY, DX, DY, color='b')

    if a**2 + b**2 + c**2 + d**2 > 0:
        X = np.linspace(-9, 9, 21)
        Y = np.linspace(-9, 9, 21)
        XX, YY = np.meshgrid(X, Y)
        DX = a * XX + b * YY
        DY = c * XX + d * YY
        ax.quiver(XX, YY, DX, DY, color='r')

    plt.show()

Püsipunktide tüübid¶

δ > 0, Δ > 0, τ > 0: ebastabiilne sõlm

Maatriksi omaväärtused on $\lambda_{1,2} = \frac{\tau}{2} \pm \sqrt{\delta}$. Mõlemad on positiivsed. Faasiportree on ebastabiilne sõlm. Püsipunkt $\underline{x}_* = (0, 0)$ on repeller.

fixed(3, 1, 1, 3)

δ > 0, Δ > 0, τ < 0: stabiilne sõlm

Maatriksi omaväärtused on $\lambda_{1,2} = \frac{\tau}{2} \pm \sqrt{\delta}$. Mõlemad on negatiivsed. Faasiportree on stabiilne sõlm. Püsipunkt $\underline{x}_* = (0, 0)$ on atraktor.

fixed(-3, -1, -1, -3)

δ > 0, Δ < 0: sadul

Maatriksi omaväärtused on $\lambda_{1,2} = \frac{\tau}{2} \pm \sqrt{\delta}$. Üks on negatiivne, üks on positiivne. Püsipunkt $\underline{x}_* = (0, 0)$ on sadul.

fixed(1, 3, 3, 1)

δ > 0, Δ = 0, τ > 0: ebastabiilne sirge

Maatriksi omaväärtused on $\lambda_1 = 0$ ja $\lambda_2 = \tau$. Üks on null, üks on positiivne. Faasiportree on ebastabiilne sirge. Püsipunkt $\underline{x}_* = (0, 0)$ on mitteisoleeritud.

fixed(1, -1, -1, 1)

δ > 0, Δ = 0, τ < 0: stabiilne sirge

Maatriksi omaväärtused on $\lambda_1 = 0$ ja $\lambda_2 = \tau$. Üks on null, üks on negatiivne. Faasiportree on stabiilne sirge. Püsipunkt $\underline{x}_* = (0, 0)$ on mitteisoleeritud.

fixed(-1, 1, 1, -1)

δ < 0, τ > 0: ebastabiilne fookus

Maatriksi omaväärtused on $\lambda_{1,2} = \frac{\tau}{2} \pm i\sqrt{-\delta}$. Nende reaalosad on positiivsed. Faasiportree on ebastabiilne fookus. Püsipunkt $\underline{x}_* = (0, 0)$ on repeller.

fixed(1, 1, -3, 1)

δ < 0, τ < 0: stabiilne fookus

Maatriksi omaväärtused on $\lambda_{1,2} = \frac{\tau}{2} \pm i\sqrt{-\delta}$. Nende reaalosad on negatiivsed. Faasiportree on stabiilne fookus. Püsipunkt $\underline{x}_* = (0, 0)$ on atraktor.

fixed(-1, 3, -1, -1)

δ < 0, τ = 0: tsenter

Maatriksi omaväärtused on $\lambda_{1,2} = i\sqrt{\Delta}$. Nende reaalosad on null. Püsipunkt $\underline{x}_* = (0, 0)$ on tsenter.

fixed(0, 1, -1, 0)

δ = 0, maatriks on diagonaalne, τ > 0: ebastabiilne sõlm

Maatriksi omaväärtused $\lambda_{1,2} = \frac{\tau}{2}$ on identsed ja positiivsed. Faasiportree on ebastabiilne sõlm. Püsipunkt $\underline{x}_* = (0, 0)$ on repeller.

fixed(1, 0, 0, 1)

δ = 0, maatriks on diagonaalne, τ < 0: stabiilne sõlm

Maatriksi omaväärtused $\lambda_{1,2} = \frac{\tau}{2}$ on identsed ja negatiivsed. Faasiportree on stabiilne sõlm. Püsipunkt $\underline{x}_* = (0, 0)$ on atraktor.

fixed(-1, 0, 0, -1)

δ = 0, maatriks on diagonaalne, τ = 0: degenereeritud

Maatriksi omaväärtused $\lambda_{1,2} = 0$ on identselt null. Faasiportree on degenereeritud. Püsipunkt $\underline{x}_* = (0, 0)$ on mitteisoleeritud.

fixed(0, 0, 0, 0)

δ = 0, maatriks ei ole diagonaalne, τ > 0: ebastabiilne tärn

Maatriksil on ainult üks positiivne omaväärtus $\lambda_1 = \frac{\tau}{2}$. Faasiportree on ebastabiilne tärn. Püsipunkt $\underline{x}_* = (0, 0)$ on repeller.

fixed(3, 1, -1, 1)

δ = 0, maatriks ei ole diagonaalne, τ < 0: stabiilne tärn

Maatriksil on ainult üks negatiivne omaväärtus $\lambda_1 = \frac{\tau}{2}$. Faasiportree on stabiilne tärn. Püsipunkt $\underline{x}_* = (0, 0)$ on atraktor.

fixed(-1, 1, -1, -3)

δ = 0, maatriks ei ole diagonaalne, τ = 0: degenereeritud tärn

Maatriksil on ainult üks omaväärtus $\lambda_1 = 0$. Faasiportree on degenereeritud tärn. Püsipunkt $\underline{x}_* = (0, 0)$ on mitteisoleeritud.

fixed(1, 1, -1, -1)

Küsimused¶

Nõrga hõõrdejõuga ühemõõtmeline lineaarne pendel¶

Ühemõõtmelist pendli kirjeldab liikumisvõrrand

$$\ddot{x} = -kx - h\dot{x}.$$

Eeldage, et $h > 0$ ja $k > \frac{h^2}{4}$. Kirjutage liikumisvõrrandi dünaamilise süsteemi kujul, kasutades definitsiooni $v = \dot{x}$. Milline on süsteemi püsipunkt $(x_*, v_*) = (0, 0)$?

ebastabiilne sõlm
stabiilne sõlm
ebastabiilne sirge
stabiilne sirge
ebastabiilne fookus
stabiilne fookus
tsenter
sadul
degenereeritud
ebastabiilne tärn
stabiilne tärn
degenereeritud tärn

Tugeva hõõrdejõuga ühemõõtmeline lineaarne pendel¶

Milliseks muutub eelnevalt kirjeldatud süsteemi püsipunkt $(x_*, v_*) = (0, 0)$, kui $0 < k < \frac{h^2}{4}$?

ebastabiilne sõlm
stabiilne sõlm
ebastabiilne sirge
stabiilne sirge
ebastabiilne fookus
stabiilne fookus
tsenter
sadul
degenereeritud
ebastabiilne tärn
stabiilne tärn
degenereeritud tärn

Ilma hõõrdejõuta ühemõõtmeline lineaarne pendel¶

Milliseks muutub eelnevalt kirjeldatud süsteemi püsipunkt $(x_*, v_*) = (0, 0)$, kui $h = 0$ ja $k > 0$?

ebastabiilne sõlm
stabiilne sõlm
ebastabiilne sirge
stabiilne sirge
ebastabiilne fookus
stabiilne fookus
tsenter
sadul
degenereeritud
ebastabiilne tärn
stabiilne tärn
degenereeritud tärn