%%html
<style type="text/css">
input.good:checked + label {color: green}
input.bad:checked + label {color: red}
input.good:checked + label::after {color: green; content: ' Õige vastus!'}
input.bad:checked + label::after {color: red; content: ' Vale vastus!'}
input[type=text]:valid {border: 1px solid green}
input[type=text]:invalid {border: 1px solid red}
input[type=text]:valid + label::after {color: green; content: ' Õige vastus!'}
input[type=text]:invalid + label::after {color: red; content: ' Vale vastus!'}
</style>

Mõisted pidevate dünaamiliste süsteemide kohta

Faasiruum

Dünaamiliste süsteemide kõige algsem mõiste on faasiruum. Faasiruum on hulk, mis koosneb kõikidest süsteemil võimalikutest olekutest. Iga faasiruumi punkt vastab identselt süsteemi olekule, ja on kirjeldatav sõltumatute muutujate kaudu. Sõltumatute muutujate arv on faasiruumi mõõde.

Näide: Ühemõõtmeline lineaarne pendel. Kui pendel liigub ainult ühes suunas, siis kirjeldab tema positsiooni üks reaalarv $x$. Aga sellest ei piisa, et pendli olekut kirjeldada, sest pendlil on lisaks positsioonile ka kiirus $v$. Positsioon $x$ ja kiirus $v$ on sõltumatud muutujad - pendlil võib olla igasugune kiirus, sõltumatu tema asukohast. Kiirendus aga ei ole neist sõltumatu, vaid järeldub pendli liikumisvõrrandist. Ühemõõtmelise pendli faasiruum on $\mathbb{R}^2$, faasiruumi mõõde on 2.

Antud näide näitab, et faasiruumi mõõde tavaliselt ei ole liikumissuundade arvuga võrdne. Tihti on faasiruum lihtsalt eukleidiline ruum $\mathbb{R}^n$, või alamhulk eukleidilisest ruumist, aga üldjuhul võib ka keerulisem olla. Näiteks, kui dünaamiline süsteem on jäik füüsikaline pendel, mis pöörleb ühes suunas ümber punkti, siis on tema positsioonide ruum hoopis ring $S^1$. Kuna kiirus on siiski reaalarv, on tema faasiruum $S^1 \times \mathbb{R}$. (Diferentsiaalgeomeetria abil võib ka õigemini öelda, et faasiruum on puutujate kihtkond $TS^1$ - mis on antud juhul võrdne ruum.)

Siit edaspidi tähistame faasiruumi tähega $Q$, ja kirjutame faasiruumi elemente kas vektori kujul või indeksitega, $\underline{x} = (x_1, \ldots, x_n)$.

Trajektoorid

Kui dünaamiline süsteem areneb ajas, siis vastab igale ajahetkele $t$ olek $\underline{x}(t) \in Q$. Funktsiooni $\underline{x}: T \to Q$, kus $T$ on lubatud ajade hulk, nimetatakse trajektooriks. Kui dünaamiline süsteem on pidev, siis on $T$ pidev ruum, ehk kas $\mathbb{R}$ või lahtine vahemik $(a, b)$.

Näide: Kui ühemõõtmeline lineaarne pendel võngub, siis on tal igal ajahetkel $t \in T = \mathbb{R}$ positsioon $x(t)$ ja kiirus $v(t)$. Võnkumise trajektoor faasiruumis on funktsioon $\underline{x}: T \to Q, t \mapsto \underline{x}(t) = (x(t), v(t))$.

Dünaamika

Lisaks faasiruumile koosneb dünaamiline süsteem ka dünaamikast. Dünaamika määrab, kuidas dünaamiline süsteem käitub, ja millised trajektoorid on lubatud. Pideva dünaamilise süsteemi dünaamikat kirjeldab diferentsiaalvõrrand. Dünaamilisi süsteeme jagatakse kahesse tüübisse:

• Autonoomse dünaamilise süsteemi dünaamikat kirjeldab diferentsiaalvõrrand $\underline{\dot{x}} = f(\underline{x})$, kus funktsioon $f$ sõltub ainult süsteemi olekust $\underline{x}$.
• Mitteautonoomse dünaamilise süsteemi dünaamikat kirjeldab diferentsiaalvõrrand $\underline{\dot{x}} = f(\underline{x}, t)$, kus funktsioon $f$ sõltub lisaks süsteemi olekule $\underline{x}$ ka ajast $t$.

Alati on võimalik ümberkirjutada mitteautonoomset süsteemi, mille faasiruum on $Q$, hoopis autonoomse süsteemina, mille faasiruum on $Q' = Q \times T$ ja mille dünaamika on $(\underline{\dot{x}}, \dot{t}) = (f(\underline{x}, t), 1)$.

Antud definitsioon väidab, et dünaamilist süsteemi kirjeldab esimest järku diferentsiaalvõrrand, kuigi näiteks pendli liikumist kirjeldab teist järku diferentsiaalvõrrand $\ddot{x} = a(x, \dot{x})$. Siin aga on juba näha et selle võrrandi muutuja on vaid positsioon $x$, kuigi faasiruum koosneb lisaks sellele ka kiirusest $v$. Dünaamilise süsteemi kujul on pendli liikumisvõrrand hoopis $(\dot{x}, \dot{v}) = (v, a(x, v))$, mis on esimest järku diferentsiaalvõrrand. Selline ümberkirjutamine on alati võimalik, kui on antud kõrgemat järku diferentsiaalvõrrand.

Algtingimused

Lisaks dünaamikale sõltub dünaamilise süsteemi käitumine ka tema olekust $\underline{x}_0 = \underline{x}(t_0)$ valitud ajahetkel $t_0$. Sellist olekut nimetatakse algtingimuseks. Dünaamika ja algtingimus koos määravad unikaalset trajektoori, mis on süsteemi liikumisvõrrandi lahendus.

Püsipunktid

Punkti $\underline{x}_* \in Q$ faasiruumis nimetatakse püsipunktiks, kui antud punktis kehtib $\underline{\dot{x}} = f(\underline{x}) = 0$ (autonoomse süsteemi kohta) või $\underline{\dot{x}} = f(\underline{x}, t) = 0$ (mitteautonoomse süsteemi kohta).

Näide: Ühemõõtmelist lineaarset pendli kirjeldab diferentsiaalvõrrandite süsteem:

• $\dot{x} = v$
• $\dot{v} = -(hv + kx)/m$

Siin $m$ on pendli mass, $k$ on vedru parameeter ja $h$ on hõõrdetegur. Kui me eeldame et need parameetrid on positiivsed, on süsteemil ainult üks püsipunkt $x_* = 0, v_* = 0$.

Kui dünaamilisel süsteemil on püsipunkt $\underline{x}_*$, siis $\underline{x}(t) = \underline{x}_*$ on unikaalne trajektoor mis vastab algtingimusele $\underline{x}_0 = \underline{x}_*$.

Vool ja faasiportree

Siit edaspidi eeldame, et dünaamiline süsteem on autonoomne, kuna igat süsteemi võib kirjutada autonoomsel kujul $\underline{\dot{x}} = f(\underline{x})$. Antud liikusmisvõrrand määrab iga faasiruumi punkti $\underline{x}$ kohta vektorit $\underline{\dot{x}}$, mis on trajektoori puutujavektor selles punktis. Kogu dünaamika on sellepärast kirjeldatav vektoriväljana faasiruumis. See vektoriväli on dünaamilise süsteemi vool. Joonistus, mis näitab dünaamilise süsteemi voolu, on faasiportree.

Näide: Ühemõõtmelise lineaarse pendli

• $\dot{x} = v$
• $\dot{v} = -(hv + kx)/m$

faasiportree on selline:

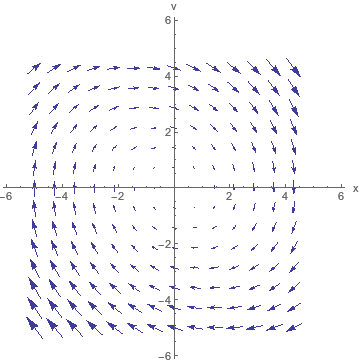
Faasiportree võimaldab leida süsteemi trajektoore graafilisel meetodil: Selleks on vaja vektoreid ühendada niimoodi, et nad on trajektooride puutujavektorid. Pendli kohta on tulemus selline:

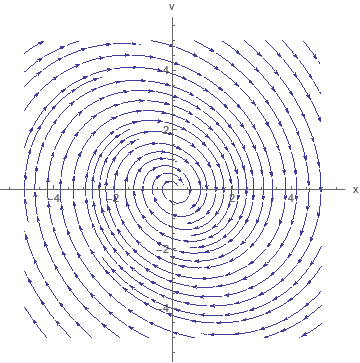
Faasiportree aitab ka leida süsteemi püsipunkte. Pendli faasiportree näitab, et ainus püsipunkt on $(x, v) = (0, 0)$.

Interaktiivne näide: ühemõõtmeline pendel

Pendli simulatsioonis kasutame SciPy integreerimiseks, NumPy numbrilisteks arvutusteks ja PyPlot joonistamiseks.

%matplotlib inline

from scipy.integrate import odeint
import matplotlib
import numpy as np
import matplotlib.pyplot as plt

Järgmisena defineerime pendli dünaamikat. See on funktsioon, mis sõltub faasiruumipunktist $y = (x, v)$, ajast $t$, hõõrdetegurist $h$, vedru parameetrist $k$ ja massist $m$:

def pendel(y, t, h, k, m):
    x, v = y
    dydt = [v, -(h * v + k * np.sin(x)) / m]
    return dydt

Konstantsed pendli parameetrid on järgnevalt.

h = 0.5
k = 0.5
m = 1

Alustame faasiportreest. Selleks on meil võrku vaja, mille peale nooli joonistada. Võrku defineeritakse NumPy funktioonidega linspace ja meshgrid.

xmin = -10
xmax = 10
nx = 21
X = np.linspace(xmin, xmax, nx)

vmin = -10
vmax = 10
nv = 21
V = np.linspace(vmin, vmax, nv)

XX, VV = np.meshgrid(X, V)

Järgmisena arvutame $(\dot{x}, \dot{v})$ igas võrgupunktis.

dxdt = np.zeros((nx, nv))
dvdt = np.zeros((nx, nv))

for i in range(nx):
    for j in range(nv):
        dxdt[i, j], dvdt[i, j] = pendel([XX[i, j], VV[i, j]], 0, h, k, m)

Lõpuks joonistame faasiportreet quiver funktsiooniga.

fig = plt.figure()
ax = fig.add_subplot(111)
ax.set_aspect('equal', 'box')
ax.set_xlabel('x')
ax.set_ylabel('v')
ax.quiver(XX, VV, dxdt, dvdt)
plt.show()

Lisaks arvutame ka trajektoori. Selleks on meil algtingimust $y_0 = (x_0, v_0)$ vaja:

y0 = [10, 0]

Järgmisena defineerime ajavahemiku $T = (t_0, t_1)$, mille vahel me süsteemi lahendame.

t = np.linspace(0, 100, 1000)

Lahenduse annab meile SciPy funktsioon odeint. Funktsiooni argumendid on dünaamika, algtingimus, ajavahemik ja konstantsed parameetrid.

sol = odeint(pendel, y0, t, args = (h, k, m))

Lõpuks joonistame trajektoori.

fig = plt.figure()
ax = fig.add_subplot(111)
ax.set_aspect('equal', 'box')
ax.set_xlabel('x')
ax.set_ylabel('v')
ax.plot(sol[:, 0], sol[:, 1])
plt.show()

Küsimused

Faasiruum ja selle dimensioon

Sfääriline pendel

Jäik füüsikaline pendel on fikseeritud ühes punktis ja võib vabalt liikuda vaid tingimusel, et vaba pendli otsa kaugus fikseeritud otsast on konstantne (ja võrdub pendli pikkusega). Mis on süsteemi faasiruumi mõõde?

• 2
• 3
• 4
• 5
• 6

Kaheosaline jäik füüsikaline pendel

Loengus vaatasime videosid, kus ühe füüsikalise pendli otsas oli fikseeritud teine füüsikaline pendel, ja iga pendel sai vabalt pöörelda ühes suunas ümber paigaldamispunkti:

Video

Milline on selle süsteemi faasiruum?

• $S^1 \times S^1 \times \mathbb{R}^2$ (toorus × eukleidiline ruum)
• $S^1 \times S^1$ (toorus)
• $\mathbb{R}^4$ (eukleidiline ruum)
• $S^4$ (neljamõõtmeline sfäär)

Trajektoorid

Palli viskamine

Keegi viskab palli ja vaatab selle liikumist. Vabalangemise tõttu jälgib pall parabooli. Kas see parabool on dünaamilise süsteemi trajektoor?

• Jah.
• Ei, palli liikumine ei ole kirjeldatav dünaamilise süsteemina.
• Ei, parabool asub ainult positsioonide ruumis, aga dünaamilise süsteemi trajektoor asub faasiruumis.

Trajektoori mõiste

Trajektoor on kirjeldatav funktsioonina…

• …mis sõltub vaid süsteemi olekust.
• …mis sõltub vaid ajast.
• …mis sõltub nii ajast kui süsteemi olekust.

Dünaamika

Dünaamika kirjeldamine võrrandi abil

Mis kirjeldab pideva dünaamilise süsteemi dünaamikat?

• Algebraline võrrand.
• Diferentsvõrrand.
• Diferentsiaalvõrrand.

Autonoomne ja mitteautonoomne süsteem

Mis on erinevus autonoomse ja mitteautonoomse süsteemi vahel?

• Autonoomse süsteemi dünaamika sõltub mitte ainult süsteemi olekust, vaid ka ajast.
• Mitteautonoomse süsteemi dünaamika sõltub mitte ainult süsteemi olekust, vaid ka ajast.
• Mitteautonoomse süsteemi dünaamika sõltub mitte ainult süsteemi olekust, vaid ka konstantsest parameetrist.

Kolmandat järku diferentsiaalvõrrand

Teile on antud diferentsiaalvõrrand $\dddot{x} = f(x, \dot{x}, \ddot{x})$, mida te soovite dünaamilise süsteemi kujul kirjutada. Mis sümbol peab olema küsimärgi asemel, et vastus oleks õige?

• $\dot{x} = v$
• $\dot{v} = a$
• $\dot{a} = f(x, v, ?)$

vastus

Algtingimused

Algtingimuse mõiste

Mis on algtingimus?

• Tingimus, millele dünaamiline süsteem peab vastama selleks, et tema dünaamika algab.
• Tingimus, millele dünaamiline süsteem peab igal hetkel vastama.
• Olek, milles dünaamiline süsteem valitud alghetkel asub.

Seos algtingimuste ja muude mõistete vahel

Milline väide on õige?

• Trajektoori määravad nii algtingimused kui süsteemi dünaamika.
• Süsteemi dünaamika määrab algtingimust.
• Trajektoor ei sõltu algtingimustest.

Püsipunktid

Püsipunktide olemasolek

Kas igal süsteemil on vähemalt üks püsipunkt?

• Jah.
• Ei.

Tuumareaktsiooni püsipunkt

Teil on tuumareaktor, milles tekib radioaktiivne aine. Olgu $x$ selle aine kogus reaktoris. Reaktoris toimuvad järgmised protsessid, mis mõjutavad aine kogust:

• Konstantne teke $a = 0,1 \mathrm{g}/\mathrm{s}$.
• Lagunemine $-kx$, kus $k$ on konstantne lagunemistegur $k = 0,01 \mathrm{s}^{-1}$.

Leidke süsteemi püsipunkti $x$.

• 1 g
• 3,18 g
• 5 g
• 10 g
• 20 g

Vool ja faasiportree

Dünaamika → faasiportree

Teile on antud dünaamiline süsteem:

• $\dot{x} = \cos y$
• $\dot{y} = \cos x$

Milline on süsteemi faasiportree?

Pilt	Faasiportree
Pilt 1
Pilt 2
Pilt 3

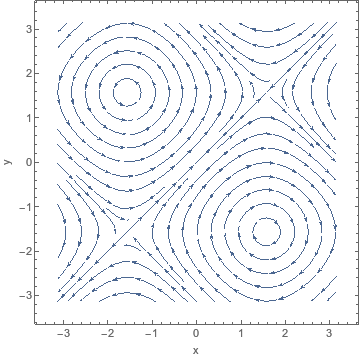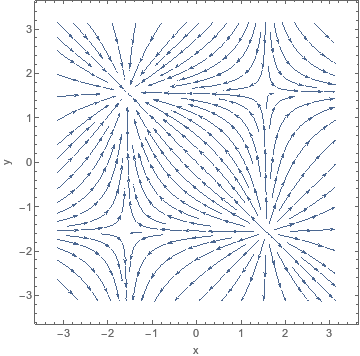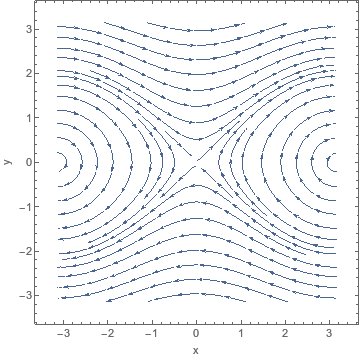Faasiportree → dünaamika

Teile on antud faasiportree:

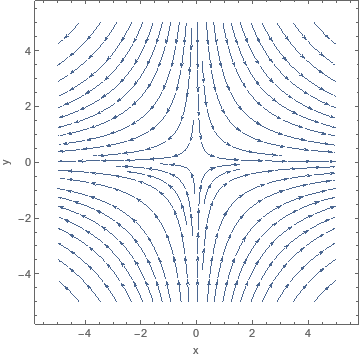
Milline on selle süsteemi dünaamika?

• $\dot{x} = x$, $\dot{y} = y$.
• $\dot{x} = x$, $\dot{y} = -y$.
• $\dot{x} = y$, $\dot{y} = x$.
• $\dot{x} = y$, $\dot{y} = -x$.